Arbre binomial

Monte-Carlo

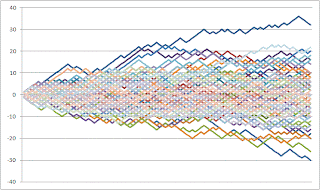
La méthode de Monte-Carlo c'est bien, ça donne un résultat mais c'est pas précis, et quand on augmente le nombre de chemins, la précision n'augmente pas beaucoup !
Si vous avez bien fait votre Monte-Carlo vous devriez trouver un résultat autour de 4.
Sur le graphique ci dessous, l'abscisse correspond au nombre de chemins, la courbe bleue à la moyenne des résultats de mes chemins, les courbes rouge et verte encadrent ma moyenne et m'indiquent que j'ai 95% de chance que la vraie valeur de ce jeu soit dans ces bornes. Au bout de 1000 chemins testés, j'ai encore 0.8 d’écart entre cette borne haute et basse, c'est énorme.

Il existe différentes techniques pour accélérer la convergence d'un Monte Carlo, mais nous ne les aborderons pas aujourd'hui.
Vous pouvez trouver mon fichier excel ici : MonteCarlo

Arbre binomial

Ce que je vous propose c'est d'opter pour une technique totalement différente.
La première étape est de faire le constat que seule la valeur finale de notre compteur est importante pour que le joueur sache combien il a gagné. Les valeurs intermédiaires ne sont pas importantes, le résultat ne dépend pas du chemin parcouru par notre compteur.

Nous allons prendre notre problème à l'envers et commencer par la fin...
Réduisons notre jeu à 3 lancers pour y voir plus clair, les valeurs finales possibles sont -3, -1, 1 et 3.
Si après le 2eme lancer notre compteur est à -2, nous savons que nous n'avons aucune chance de gagner quoi que ce soit, car nous finirons soit à -3 soit à -1, donc notre résultat sera forcement 0. Nous pouvons donc dire que le prix du jeu au bout de 2 lancers si notre compteur arrive à -2 est 0. On peut arrêter de jouer, ça sert plus à rien.
Par contre si après le 2eme lancer nous sommes à 0, les choses sont plus intéressantes, on a une chance sur 2 de gagner 1euro. Comme nous l'avons vu dans le premier post, la valeur que nous sommes prêt à payer pour avoir 1/2 chance de gagner 1 euro, c'est 0.5euros. Donc si notre compteur est á 0 au deuxième lancer, notre jeu vaut 0.5 euro. Si on arrête de jouer, on perd en moyenne 0.5 euro.
Voyons le dernier cas, si notre compteur est á 2, alors on est sûr de gagner quelque chose, soit 3 soit 1. une demi chance de gagner 3, une demi chance de gagner 1, le jeu vaut donc en moyenne 2.
pour résumer apres le 2eme lancer :
si on est à -2 le jeu vaut 0
si on est à 0 le jeu vaut 0.5
si on est à 2 le jeu vaut 2
Maintenant voyons ce qui se passe après le 1er lancer, notre compteur est soit à 1 soit à -1.
s'il est à -1, alors on a une chance sur deux qu'il passe à -2 et que le jeu perde toute valeur, et une chance sur deux que le compteur passe à 0 et que le jeu vaille 0.5. donc si apres le 1er lancer notre compteur vaut -1, alors notre jeu vaut 0.25.
S'il est a 1, alors 1/2 chance de passer à 0 (oú le jeu vaut 0.5), 1/2 chance de passer à 2 (oú le jeu vaut 2), donc notre jeu vaut 1.25.
Nous arrivons au début du jeu et en suivant la même logique nous déduisons la valeur du jeu : 0.75euro

Pour résumer : (en bleu le compteur, en rouge le prix)

Maintenant on peut se poser la question de savoir si ça va pas être horriblement long à calculer.
Pour savoir cela nous devons connaitre le nombre d’opérations à effectuer. On fait une opération à chaque fois que l'on fait la moyenne de deux prix.
Si N est notre nombre de lancers, nous avons N+1 opérations à faire pour faire la première étape (les calculs lors du dernier lancer) puis N, puis N-1, puis N-2, etc... jusqu’à 1.
Or la somme de (N+1)+N+(N-1)+(N-2)+...+1 ça fait (N+1)*N/2
Donc pour 100 lancers : 5050 opérations c'est à dire quasiment rien.

La solution exacte arrive...

Vous allez donc pouvoir tester cet algorithme sur Excel pour passer d'une solution approximative lente à calculer (MonteCarlo) à la solution exacte rapide à calculer !
Cette méthode semble idéale, mais elle a quelques problèmes dans le cas général...
Premièrement, l'algo peut nous trouver la solution exacte car nous sommes dans un cas simple: une pièce de monnaie ne prend que 2 valeurs. En finance la valeur d'une action peut prendre une infinité de valeurs ! Si nous voulons y utiliser cet algo, il faut supposer que le prix d'une action ne peux prendre qu'un nombre fini de valeur ! cela introduit une approximation et donc une erreur !
Deuxièmement, la méthode n'est utilisable que si le résultat final ne dépend pas du chemin pris par notre compteur. Nous verrons cette limitation dans un prochain exercice !
Il y a d'autre probleme qui se pose sous certaines conditions, mais on verra ça plus tard !
A vos Excel, vous devez maintenant pouvoir sortir la vraie valeur de ce jeu !

Montecarlo

Les options européennes

Notre petit jeu du post précédent ressemble à des options de type européennes, ces options payent la performance d'une action si cette performance est positive.
Pourquoi européennes ? Car il existe plusieurs types d'options : Américaines, Asiatiques, Bermudéennes. Nous verrons peut-être la différence une autre fois.

Alors quel est le prix de ce petit jeu ? pour le savoir il faut connaitre combien on a de chances d'arriver à chaque résultat. Pour connaitre ce nombre de chances il faut compter le nombre de chemins qui y mènent et diviser par le nombre total de chemins.

La solution

Par exemple pour arriver au résultat +5, il n'y a qu'un seul chemin : pile pile pile pile pile (on va résumer par PPPPP).
Pour le résultat +3, il y'en a beaucoup plus : PPPPF, PPPFP, PPFPP, PFPPP, FPPPP nous avons donc 5 fois plus de chances de finir sur +3 que sur +5.
Pour le résultat +1, il y a 10 chemins (là je vous demande de me croire :))
Pour les résultats négatifs c'est la même chose (on a autant de chance que la pièce soit pile que face !)
Donc -1 : 10 chemins, -3 : 5 chemins, -5 : 1 chemins
Soit un total de 32 chemins

Donc nous avons 1/32 chances de faire +5, 5/32 chances de faire +3, 10/32 chances de faire +1, etc...
Si on multiplie chacune de ces probabilités avec ce que ces chemins rapportent cela nous donne :
1/32*5 + 5/32*3 + 10/32*1 + 10/32*0 + 5/32*0 + 10/32*0
Pourquoi multiplier par 0 les derniers termes ? car si le compteur est négatif, on ne gagne rien !
Donc nous avons : 0.9375
Ce chiffre correspond à la vrai valeur de ce jeu d'un point de vue neutre par rapport au risque.
Donc si on vous propose 1 euro pour jouer vous pouvez vous dire que c'est un peu cher. Certes vous pouvez gagner 5 euro, mais vous avez beaucoup plus de chance de ne rien gagner du tout !

On augmente le nombre de lancer !

Maintenant supposons que notre jeu continue et que plutôt que de faire 5 lancers, nous en faisons 100.
Compter tous les chemins devient impossible... si vous pouviez compter un milliard de chemins par seconde (une performance digne d'un supercalculateur) il vous faudrait environ 40 milliards d’années... hum... on va peut être utiliser une autre méthode !!!
La méthode que je vais vous proposer est loin d’être la meilleure car notre problème peut se résoudre très simplement par une analyse mathématique plus poussée. Mais c'est une méthode très générale qui est massivement utilisée en finance.
Plutôt que de compter tous les lancers, il suffit de jouer à ce jeu un certains nombre de fois et de faire la moyenne de nos gains. Si vous jouez 100 fois à un jeu et que vous constatez que vous gagnez en moyenne 5 euros, alors vous pouvez faire l'approximation que ce jeu vaut 5 euros. C'est la méthode de MonteCarlo (la légende veut que l'inventeur de la méthode ci dessus avait un oncle accroc au casino).

Donc pour utiliser cette méthode soit vous lancez 100000 fois votre pièce (attention à ne pas perdre le compte ! Sinon il y a un biais dans le calcul et il faut tout recommencer !), ou alors vous laissez le soin à un logiciel de faire les lancer.
Pour cela le plus simple c'est un tableur, comme Excel ou celui fournit dans la suite OpenOffice.
Pour faire un lancer il suffit de tirer un nombre aléatoire :
pour Excel en français c'est :
=ALEA()
Cela nous renvoi un nombre aléatoire entre 0 et 1. Nous voulons un pile ou un face. C'est à dire 0 ou 1.
Puisqu'on a autant de chance d'avoir pile ou face, et qu'il y'a autant de chance que notre nombre aléatoire soit plus petit ou plus grand que 0.5, nous pouvons faire cela :
=SI(ALEA()<0.5,0,1)
maintenant que vous pouvez lancer une pièce avec Excel, vous pouvez créer votre compteur par dessus puis étendre votre formule sur autant de cases que nécessaire !
Attention tout de même car Excel c'est simple, mais c'est pas efficace, 10000 chemins avec 100 lancers chacun ça vous fait 1 000 000 cellules à calculer et à stocker, vous allez vite le mettre à genoux ! Donc quelques précautions à prendre :

• Sauvegarder
• Désactiver le calcul automatique dans outils->option (gros bouton en haut à gauche sur les nouveaux Excel) Pour calculer faites F9
• Sauvegarder souvent  (vous allez faire planter Excel)
• Allez y petit à petit (1000 chemins du premier coup c'est pas une bonne idée)
• Sauvegarder très souvent  (Excel fini toujours par planter)
• Utiliser un maximum les possibilités des formules d'Excel pour pouvoir étendre simplement vos formules et passer de 5 a 1000 chemins en un rien de temps ! (enfin, sauf pour les calculs...)

Rendez vous la prochaine fois pour la solution ! (Et peut être le fichier Excel si je trouve un moyen de le stocker)

Introduction

Pourquoi ce blog ?

Premièrement, j'ai pris l'habitude de choisir au hasard les décisions insolubles (comme par exemple : j’achète Civilization 5 ou Fallout New Vegas ?). Pour repondre a ces questions existentielles, rien de tel qu'une pièce de monnaie. Pile ou face ? Parfois prendre une décision rapidement est mieux que de prendre la décision parfaite au bout d'une heure ! Et souvent le fait que la pièce va apporter la réponse me pousse à prendre rapidement ma propre décision.

Deuxièmement, je suis Quant et personne ne comprend ce que je fait (sauf les autres Quants). Donc via ce blog, j’espère pouvoir répondre de façon ludique aux interrogations de ma famille et de mes amis sur mon métier. 

Combien êtes-vous prêt à payer pour jouer à de petits jeux de hasard basés sur des lancer de pièces de monnaies ? Car avec ces petites pièces, on peut recréer les mêmes problématiques que sur les marchés financiers.

Etre neutre risque vis a vis du risque

Pour commencer, combien êtes-vous prêt à payer pour jouer à un jeu qui vous rapporte 1euro si la pièce tombe sur pile et rien si elle tombe sur face ? Si vous êtes prêt à payer 0.50euro c'est que vous êtes neutre face au risque. Si vous êtes prêt à payer plus que 0.50euro vous aimez le risque. Si vous êtes prêt à payer moins de 0.50euro vous êtes averse au risque.

Le comportement cohérent sur les marchés financiers c'est l'aversion au risque.

Le comportement cohérent au casino (pour le joueur) c'est l'amour du risque.

Mais pour la finance comme pour le casino, il y a deux personnes qui jouent : Le vendeur et l'acheteur; Le croupier et le joueur. Le comportement ne s’éloigne donc jamais beaucoup de la neutralité.

Donc je pars de la base que vous êtes prêt à payer 0.50 euro pour gagner 1euro si la pièce tombe sur pile.

Commençons les choses intéressantes...

On va garder en mémoire un petit compteur qui vaut 0 au départ.

Maintenant, on lance notre pièce... 

elle tombe sur pile => on ajoute 1 au compteur

elle tombe sur face => on enlève 1 au compteur

Répétons cela une deuxième fois, notre compteur peut prendre les valeurs : 2, 0 ou -2

Une troisième fois, notre compteur peut prendre les valeurs : 3,1,-1,3

Une quatrième fois, notre compteur peut prendre les valeurs : 4,2,0,-2,-4

Une cinquième fois, notre compteur peut prendre les valeurs : 5,3,1,-1,-3,-5

Si je vous propose de jouer à un jeu ou l'un d'entre nous recevra la valeur du compteur si celui si est positif (5,3 ou 1) et 0 dans le cas négatif.

Combien êtes-vous prêt à payer pour jouer à ce jeu ?

Combien êtes-vous prêt à payer pour vendre ce jeu ?

Les deux réponses sont les mêmes si nous sommes neutre face au risque.

Je vous attends au prochain poste pour la solution !